Proyecto Rutas óptimas

Resumen

El presente s sitio es el resultado del proceso realizado por el equipo de rutas óptimas, el cual resume el trabajo desarrollado por un grupo multidisciplinario de profesionales el 2020 y que fue liderado por el Subdepartamento de Investigación Estadística. Dicho proceso dio como resultado el documento titulado Rutas óptimas para recolectores del IPC del cual, el documento que se presenta a continuación, es su parte aplicada. Los hitos del proceso describen la elección de un algoritmo genético que permite ordenar la cercanía entre los nodos y dibujar la ruta que debe seguir un recolector del IPC sobre los lugares asignados. Dicha implementación fue estadísticamente significativa, la reducción en los tiempos de viaje fue del 15% en un total de 161 puntos en el espacio.

Usaremos algoritmos genéticos (AG) para resolver el problema de vendedor ambulante. Incorporaremos este método que utiliza un proceso iterativo de 100 soluciones de algoritmos genéticos. Por lo tanto, seleccionaremos lo mejor de todos esos procesos para resolver un TSP simple con 10 puntos espaciales. También tenemos que los AG son un método de optimización o algoritmo de búsqueda. En este sentido, un algoritmo de búsqueda puede exhibir un comportamiento heurístico si se ejecuta de manera continua, adaptándose a la dinámica del entorno en el que se utiliza, exhibiendo de este modo una conducta de aprendizaje.

Se ilustra el proceso de generación de rutas óptimas mediante el software de programación R¹ a través del uso de un algoritmo genético (AG) creado mediante la librería GA², el cual es aplicado mediante una serie de cien simulaciones de las que se escoge la que converge a un óptimo. La aplicación del AG es estimada sobre una matriz de distancias geográficas de la cual se construye la ruta que recorre las calles de Chile a través de un Motor de Rutas de código abierto (OSRM³) programado originalmente en C++ y que fue implementado sobre un contenedor Docker⁴ el que fue implementado mediante línea de comando en el Terminal del sistema operativo Linux Ubuntu⁵ en la búsqueda de solución a rutas o recorridos para los recolectores de datos en terreno.

Introducción

Originalmente conocido como el problema del vendedor viajero (TSP para abreviar), la idea es encontrar la forma más económica de visitar todos los lugares y regresar -o no- al punto de partida. La forma de visitar todos los lugares es simplemente el orden en que se visitan dichos puntos, el recorrido se denomina tour o circuito por dichos puntos, tal como lo define Flood (1956).

Este ejercicio que suena modesto es de hecho uno de los problemas más intensamente investigados en matemáticas computacionales, manifiesta Little et al. (1963). Ha inspirado estudios matemáticos, informáticos, químicos, físicos y una amplia variedad de investigaciones. Los profesores de algunos colegios en el mundo utilizan el TSP para introducir matemáticas discretas en las escuelas primarias, intermedias y secundarias, así como en universidades y escuelas profesionales. El TSP ha tenido aplicaciones en las áreas de logística, genética, fabricación, telecomunicaciones y neurociencia, por nombrar solo algunas disciplinas, según Applegate et al. (1998).

Por otro lado, Jaffee (1996) manifiesta que el atractivo del TSP lo ha elevado a uno de los pocos problemas contemporáneos de las matemáticas para convertirse en parte de la cultura popular. Su interesante nombre seguramente ha jugado un papel, pero la razón principal del gran interés es el hecho de que este modelo de fácil comprensión aún elude una solución general. La simplicidad del TSP, junto con su aparente intratabilidad, lo convierte en una plataforma ideal para desarrollar ideas y técnicas para abordar problemas computacionales en general.

Breve historia del problema del vendedor viajero

El origen del nombre “problema del vendedor viajero” es misterioso. No parece haber ninguna documentación que señale al creador del nombre, y es desconocido cuándo entró en uso por primera vez. Uno de los primeros investigadores de TSP y uno de los más influyentes fue Merrill Flood en EE.UU. Sin embargo, también existen registros previos en Alemania y en Suiza en relación al mismo tipo de problema, según Applegate et al. (2003).

En la década de 1950, el nombre de TSP se usaba ampliamente. La primera referencia que contiene el término parece ser un informe de 1949, “Sobre el juego hamiltoniano (un problema de los vendedores viajeros)”, pero parece claro por el escrito no se estaba introduciendo el nombre. Sin embargo, es posible mencionar que en algún momento durante la década de 1930 o 1940, muy probablemente en Princeton, el TSP tomó su nombre y los matemáticos comenzaron a estudiar el problema en serio, según Applegate et al. (2003).

Algunos registros históricos obtenidos desde Applegate et al. (2003) muestran lo llamativo del problema del vendedor viajero:

Algoritmo genético

La idea subyacente de un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema específico. En los años 70’s, de la mano de John Henry Holland, surgió una de las líneas más prometedoras de la inteligencia artificial, la de los algoritmos genéticos, (AG). Son llamados así porque se inspiran en la evolución biológica y su base genético-molecular (Mirjalili (2019)). Estos algoritmos hacen evolucionar una población de individuos (para este caso particular, recorridos) sometiéndola a acciones aleatorias semejantes a las que actúan en la evolución biológica (mutaciones y recombinaciones genéticas), así como también a una selección de acuerdo con algún criterio, en función del cual se decide que recorridos son más adaptados, que “sobreviven,” y cuáles los menos aptos, que son descartados.

Charles Darwin una vez dijo en su libro, el origen de las especies: “No es la más fuerte de las especies la que sobrevive, ni la más inteligente, sino la que mejor responde al cambio” Darwin (1859). En este sentido debemos comprender el concepto de “evolución” en el contexto del machine learning y así entender el mecanismo de funcionamiento de este algoritmo.

Por lo tanto, el algoritmo genético es un procedimiento adaptativo basado en los mecanismos de genética natural y selección natural. El algoritmo genético tiene dos componentes esenciales: ajuste a la sobrevivencia y diversidad genética. Originalmente desarrollado por Holland (1975), el algoritmo Genético (AG) es una búsqueda heurística que se asimila al proceso de la evolución natural. Usa el concepto de “Selección natural” y “Genética inherente” de Darwin (1859). Actualmente existen una infinidad de aplicaciones de algoritmos Genéticos como optimización y resolución de problemas de agendamiento, ingeniería del espacio aéreo, astronomía y astrofísica, química, ingeniería eléctrica, mercados financieros, ingeniería de materiales, biología molecular, reconocimiento de patrones y minería de datos y robótica, solo por nombrar algunas áreas donde se aplica.

En nuestro caso, el algoritmo genético (AG) es usado para resolver el TSP. Sin embargo, agregamos un componente adicional. Es decir, generamos 100 simulaciones de algoritmos genéticos que buscan soluciones, que luego se contrastan y selecciona la respuesta que más veces se repite en el total de simulaciones, con el fin de obtener el mejor resultado posible. Este componente adicional entrega el carácter de aprendizaje al proceso de búsqueda de soluciones.

Funcionamiento en R

R Core Team (2020) es el proyecto que sustenta el Software estadístico R, en el existe todo un esquema de trabajo que permite la creación de un proceso de implementación limpio del problema del vendedor viajero. Este proceso comienza con la lectura de las librerías que nos permiten trabajar con bases de datos (Wickham and Bryan (2019), Wickham et al. (2020) y Bittinger (2020)) y bases de datos espaciales (Bivand, Pebesma, and Gomez-Rubio (2013) y Pebesma (2018)) por un lado y por el otro, un conjunto de librerías que nos permiten el procesamiento de dicha información espacial mediante el algoritmo genético (Scrucca (2012)) y creación y mapeo de la ruta resultante (Giraud (2020) y Cheng, Karambelkar, and Xie (2019)). Antes que todo, un aspecto crucial es la puesta en marcha de un sistema operativo Linux Ubuntu (Raggi, Thomas, and Van Vugt (2011)) que nos permite la implementación de un motor de ruteo de código abierto (proyecto OSRM, Huber and Rust (2016)) el que, a su vez, nos obliga a la ejecución de un contenedor Docker (Boettiger (2015)). Para conocer las bondades de trabajar con contenedores y en especial Docker, se recomienda revisar aspectos generales en el sitio web de la aplicación.

Por lo tanto, debemos tener acceso a un conjunto de elementos necesarios para ejecutar el proceso. Los componentes necesarios son: un sistema operativo Linux-Ubuntu, R (con sus librerías), Rstudio y OSRM implementado en contenedor Docker. El proceso está compuesto de cuatro etapas; la primera corresponde a la lectura de las bases de datos espaciales, las que permiten la identificación de los puntos de los lugares a visitar, que deben estar correctamente determinados geoespacialmente. En el caso de Chile, estos puntos son determinados mediante estándares espaciales debidamente implementados, que en nuestro caso fue tarea del Departamento de Geografía, quienes nos hicieron entrega de los puntos latitud y longitud de cada establecimiento. La segunda etapa, corresponde al procesamiento de una matriz de distancias mediante un método que incluye la participación de cien algoritmos genéticos, este proceso considera una combinación de todas las soluciones de que se extrae la que mejor respuesta; la tercera etapa es la generación de la ruta producto del ordenamiento espacial previamente calculado mediante un motor de rutas (OSRM) que permitirá utilizar datos reales (provenientes de Open Street Map) conocidos para moverse entre un punto y otro; y la cuarta y última etapa es el mapeo de la solución en un mapa interactivo.

En este informe la determinación geoespacial se realizará mediante la librería tmaptools (Tennekes (2020)) a través de la función geocode_OSM, que usa el estándar definido para los datos distribuidos mediante OSM (Bennett (2010)) y que pueden ser revisados en su documento oficial⁶. Además, del uso que daremos debemos cumplir con no sobredemandar estos servidores que tienen un uso no-intensivo, ya que podríamos ser bloqueados en caso que hagamos un uso intensivo. Por otro lado, con el fin de resguardar la información que maneja el INE, usaremos direcciones y puntos espaciales correspondientes a sitios no sensibles y museos (10 en total) localizados en el centro de Santiago. De esta forma, evitamos publicar información que pueda ser privada o sensible y al mismo tiempo, no sobredemandamos a los servidores públicos del proyecto OSM⁷.

Motor de ruteo (OSRM)

Un motor de ruteo es un sistema que, a partir de un listado de puntos espaciales ordenados, devuelve un recorrido por las calles, el tipo de transporte, el tiempo y la distancia total recorrida. Por lo tanto, en el mundo del mapeo web, el camino hacia la realidad del cálculo optimizado de rutas es uno de los grandes desafíos. No se trata solamente de ir del punto \(A\) hacia el punto \(B\), sino de proponer varias opciones, itinerarios alternativos, tomar en cuenta las diferentes modalidades de transporte (automóvil, caminata, tren, bicicleta, bote, etc.), incluir etapas, respetar los sentidos de las calles. De este modo, el surgimiento de los equipos móviles refuerza la importancia de estos servicios, cuya eficiencia depende de la calidad de los datos utilizados.

En esta experiencia, Google Maps no es una opción de trabajo en una institución del Estado. Luego de investigar diferentes alternativas, nos decantamos por la idea de armar un motor de itinerarios, libre y gratis, específico y muy conveniente para nuestra realidad, muchas veces limitada en recursos económicos.

El mapa esquemático que describe el proceso de implementación considera el trabajo mediante el sistema operativo Linux Ubuntu 20.04 (Petersen (2020)), el cual fue implementado luego en un servidor Linux Centos en la institución. Este proceso, primero necesitó la instalación de la herramienta Docker (Boettiger (2015)), que es un sistema de contenedores que permitirá la consulta (mediante una API generada) de las rutas cuando es puesto en marcha el software del proyecto OSRM (Giraud (2020)). En esta sección, detallamos el proceso usado para armar el motor de enrutamiento.

Inicios del proyecto OSRM

En inglés Open Source Routing Machine (OSRM), significa que es una máquina de enrutamiento de código abierto y corresponde en otras palabras a un servidor de enrutamiento diseñado para usar con los datos aportados desde el proyecto OpenStreetMap (OSM) también del mundo del software libre.

El proyecto OSRM mostró sus primeros frutos el 9 de julio de 2010, construido completamente por el trabajo desarrollado por Dennis Luxen. El siguiente año, Luxen presenta sobre OSRM en la conferencia GIS ’11 de ACM junto con Christian Vetter⁸ Actualmente el equipo de enrutamiento de Mapbox continúa el proyecto, manteniendolo y desarrollandolo (Detomasi, Mathieu, and Botto (2018)).

Características

En contraste con la mayoría de servidores de enrutamiento, OSRM (Giraud (2020)) no utiliza una variante de A* para calcular la ruta más corta, sino que usa las jerarquías de contracción. Esto da como resultado tiempos de consulta muy rápidos, normalmente por debajo de 1 milisegundo para conjuntos de datos grandes sobre los mil nodos. Por eso, OSRM es en un buen candidato para las aplicaciones y sitios de enrutamiento receptivos basados en la web. Sus características son:

• Enrutamiento muy rápido
• Altamente portable
• Formato simple de datos que facilita la importación personalizada de conjuntos de datos en lugar de datos de OpenStreetMap o la importación de datos de tráfico
• Perfiles flexibles de enrutamiento (p.ej., para varios medios de transporte)
• Interpreta las restricciones de giro, incluyendo las restricciones condicionales basadas en el tiempo
• Interpreta los carriles de giro
• Instrucciones de conducción localizadas por OSRM

Servicios y aplicaciones que usan OSRM

• ES:Cycle.travel – direcciones en bicicleta
• Maps.Me – direcciones y mapas móviles fuera de línea
• Las API asociadas a OSRM son usadas por varios servicios webs, tales como RunKeeper
  • MapboxDirections.swift en las plataformas de Apple como iOS
  • Mapbox Servicios de Java en Java SE y Android
  • Mapbox JavaScript SDK en el navegador y Node.js
  • Mapbox Unity SDK

Implementación de Docker

Como siempre en estos temas, Google Maps fue uno de los pioneros a proponer un servicio eficiente de gran escala. Sus datos y su servicio son relacionados a una política comercial y propietaria. Igualmente, en otros competidores: Bing Maps, Yahoo Maps, ArcGis, etc.

Buscábamos un sistema que funcione independiente y gratis, así que hemos elegido OSRM (Open Source Routing Machine), que es basado sobre los datos de OpenStreetMap (OSM). No es la única solución que existe para calcular itinerarios, pero es muy sencillo de implementar y sobre todo es muy potente. La página oficial del proyecto puede ser visitada aquí http://project-osrm.org/

Creado por Dennis Luxen del Instituto Tecnológico de Karlsruhe, OSRM (Giraud (2020)) es programado mayormente en C++ y compatible con la mayoría de los sistemas operativos (Linux, FreeBSD, Windows, Mac).

El OSRM está basado sobre datos viales y de la calidad de estos datos va a depender la calidad del resultado. Como siempre en los datos espaciales, dos puntos son importantes, la geometría y los atributos. La geometría es lo más obvio de entender porque es visual y se comprende perfectamente sí una calle no está presente en nuestra base de datos, nuestro algoritmo no podrá darnos una ruta que pase por ella. En cuanto a los atributos su rol es diferente pero su importancia es igual. En efecto, una base de datos que contiene informaciones (es decir campos) sobre el sentido del tráfico, la velocidad máxima autorizada o el número de carriles ofrecerá mucho más potencial que una que contiene únicamente la geometría y el nombre de las vías.

La ventaja de los datos abiertos va adelante de la cuestión del precio (aunque no es despreciable cuando se sabe el costo importante de una base de datos vial propietaria), pero también con la filosofía de tener la libertad de modificar dichos códigos en caso que sea necesario, la opción siempre está abierta. El modelo OSM funciona perfectamente (hay que ver la cantidad y calidad de datos en Europa y EE. UU), la mejor prueba de eso fue de Map Maker de parte de Google que permite a los usuarios editar (agregar, suprimir, modificar), ahora en base a los datos de Google Maps. La diferencia es que estos datos creados por el usuario son propiedad de Google y no de él, ni de una comunidad.

Docker en Ubuntu 20.04

Primero debemos hacer la instalación del software Docker sobre nuestro sistema, utilizando para estos efectos el terminal del sistema Linux Ubuntu. Al cual, mediante dicho terminal, podemos hacer la instalación de Docker. Los pasos y el proceso considera las siguientes etapas.

Instalación y puesta en marcha

Para instalar el motor de Docker, necesitamos una versión de 64-bit de Ubuntu, en nuestro caso Ubuntu 20.04. El motor de Docker es soportado en arquitecturas x86_64 (o amd64), armhf, y arm64. En este caso instalamos usando el repositorio.

Antes de instalar el motor de Docker por la primera vez en nuestro equipo hospedador, debemos definir el repositorio de Docker. Después, podemos instalar y actualizar Docker desde el repositorio.

Definiendo el repositorio

+ Actualiza el paquete apt indice e instalamos los paquetes para permitir apt el uso del repositorio sobre HTTPS:

$ sudo apt-get update

$ sudo apt-get install \
    apt-transport-https \
    ca-certificates \
    curl \
    gnupg-agent \
    software-properties-common

Agregando la llave GPG oficial de Docker

$ curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add -

Verificamos que ahora tenemos la llave con la huella 9DC8 5822 9FC7 DD38 854A E2D8 8D81 803C 0EBF CD88, mediante la verificación que coincidan los últimos 8 digitos.

$ sudo apt-key fingerprint 0EBFCD88

pub   rsa4096 2017-02-22 [SCEA]
      9DC8 5822 9FC7 DD38 854A  E2D8 8D81 803C 0EBF CD88
uid   [unknown] Docker Release (CE deb) <docker@docker.com>
sub   rsa4096 2017-02-22 [S]

Instalando el motor Docker

• Actualizamos las librerías de Ubuntu, e instalamos la última versión del motor Docker.

 $ sudo apt-get update
 $ sudo apt-get install docker-ce docker-ce-cli containerd.io

Verificación de la instalación

• Con el siguiente comando, verificamos que resulta la palabra “Hello-World.”

$ sudo docker run hello-world

Este comando descarga una imagen de prueba y la ejecuta en un contenedor. Cuando el contenedor se ejecuta, este imprime el mensaje informal y termina.

El motor de Docker está instalado y corriendo. El grupo docker es creado pero no hay incorporación de usuarios. Debemos usar el comando sudo para ejecutar Docker. Continuamos con la instación desde Linux para permitir que los usuarios sin privilegios ejecuten comandos de Docker y para otros pasos de configuración opcionales.

OSRM para mapas de Chile

En esta etapa debemos dirigirnos al sitio web de Github del proyecto OSRM. Luego usando el terminal de Ubuntu debemos seguir los pasos.

Usando Docker

Utilizamos las imagenes de OSRM de Docker (backend, frontend) en Debian y nos aseguramos de que sean lo más ligeras posible.

Descargamos los mapas de Chile desde OpenStreetMap, por ejemplo, de Geofabrik. Este mapa es actualizado regularmente con la información aportada por la comunidad chilena y que alimenta de información geoespacial estas bases de datos.

wget http://download.geofabrik.de/south-america/chile-latest.osm.pbf

Pre-procesamos el extracto con el perfil e inicializamos un servidor HTTP del motor de enrutamiento en el puerto 5000 con el siguiente comando de Docker.

docker run -t -v "${PWD}:/data" osrm/osrm-backend osrm-extract -p /opt/car.lua /data/chile-latest.osm.pbf

La marca -v crea el directorio “/data” adentro del contenedor de Docker y lo hace disponible ahí. El archivo “/data/chile-latest.osm.pbf” dentro del contenedor es referenciado en “/chile-latest.osm.pbf” en el servidor.

Ejecutamos:

docker run -t -v "${PWD}:/data" osrm/osrm-backend osrm-partition /data/chile-latest.osrm
docker run -t -v "${PWD}:/data" osrm/osrm-backend osrm-customize /data/chile-latest.osrm

Note que chile-latest.osrm tiene una extensión de archivo diferente.

docker run -t -i -p 5000:5000 -v "${PWD}:/data" osrm/osrm-backend osrm-routed --algorithm mld /data/chile-latest.osrm

Hacemos las consultas en el servidor HTTP

Una vez el servidor OSRM esta activo y funcionando para recibir consultas de rutas. Este es posible usarme mediante la librería de R llamada OSRM. En este caso, consideraremos algunos puntos georefenciados en torno a la ciudad de Santiago, las que serviran como un ejemplo del uso del OSRM.

En esta etapa cargamos las librerías, se definen dos direcciones de INE y museos en Santiago, para luego obtener mediante OSM las coordenadas geográficas y luego construir un dataframe con dicha información.

#Ejecución de las librerías
library(tmaptools)
library(leaflet)
library(osrm)

# Listado de direcciones para geolocalizar
museos<-c("Morande 801, Santiago, Santiago",
         "Paseo Bulnes 418, Santiago",
         "José Miguel de La Barra 650, Santiago",
         "Matucana 501, Santiago",
         "Portales 3530, Santiago, Estación Central, Región Metropolitana",
         "Av Vicuña Mackenna 37, Santiago, Región Metropolitana",
         "Plaza de Armas 951, Santiago, Región Metropolitana",
         "José Victorino Lastarria 307, Santiago, Región Metropolitana",
         "Av. República 475, Santiago, Región Metropolitana",
         "Fernando Márquez de La Plata 0192, Providencia, Región Metropolitana")

# Con esta función hacemos la consulta directo a Open Street Maps
# geodato<-geocode_OSM(museos)

# Con el fin de no sobrecargar el servidor OSM por unica vez hacemos la consulta
# Luego, guardamos un archivo rds para luego utilizarlo.

geodato<- readRDS("geodatos.RDS")

# Seleccionamos la dirección y la referencia espacial.
locs<-data.frame(id=geodato$query, lat=geodato$lat, lon=geodato$lon)

Primera visualización de los datos en el espacio.

library(htmlwidgets)
library(webshot)
library(leaflet)
# Visualizamos en el espacio la ubicación de los museos
m<-leaflet(data = locs) %>% addTiles() %>%
  addMarkers(~lon, ~lat, popup = ~as.character(id), label = ~as.character(id))

m

Mapa de los puntos sin optimizar

En la Figura visualizamos mediante la librería leaflet los puntos en el espacio. Esta función crea un widget de mapa utilizando htmlwidgets. El widget se puede representar en páginas HTML generadas a partir de R Markdown, Shiny u otras aplicaciones.

Mediante el uso de la librería sf construimos un objeto tipo dataframe con atributos espaciales. En su forma más básica, un objeto sf es una colección de características simples que incluye atributos y geometrías en forma de dataframe. En otras palabras, es un dataframe (o tibble) con filas de entidades, columnas de atributos y una columna de geometría especial que contiene los aspectos espaciales de las entidades. Este formato es necesario para usar en OSRM.

# Se construye un objeto espacial de los 10 museos
library(sf)
locs <- structure(
  list(id=geodato$query,lon = geodato$lon,  lat = geodato$lat), 
  class = "data.frame", row.names = c(NA, -10L))

Mediante la función osrmRoute hacemos una ruta sin orden, ni optimizada con el fin de evidenciar que el uso de OSRM no genera ningú tipo de optimización de rutas.

# Se estima una ruta entre los museos usando la función osrmRoute
ruta1 <- osrmRoute(loc = locs, returnclass = "sf")
plot(st_geometry(ruta1), col = "red", lwd = 2)
points(locs[,2:3], pch = 20, cex = 3)
text(locs[,2:3],as.character(row.names(geodato)), cex = .8, col="grey")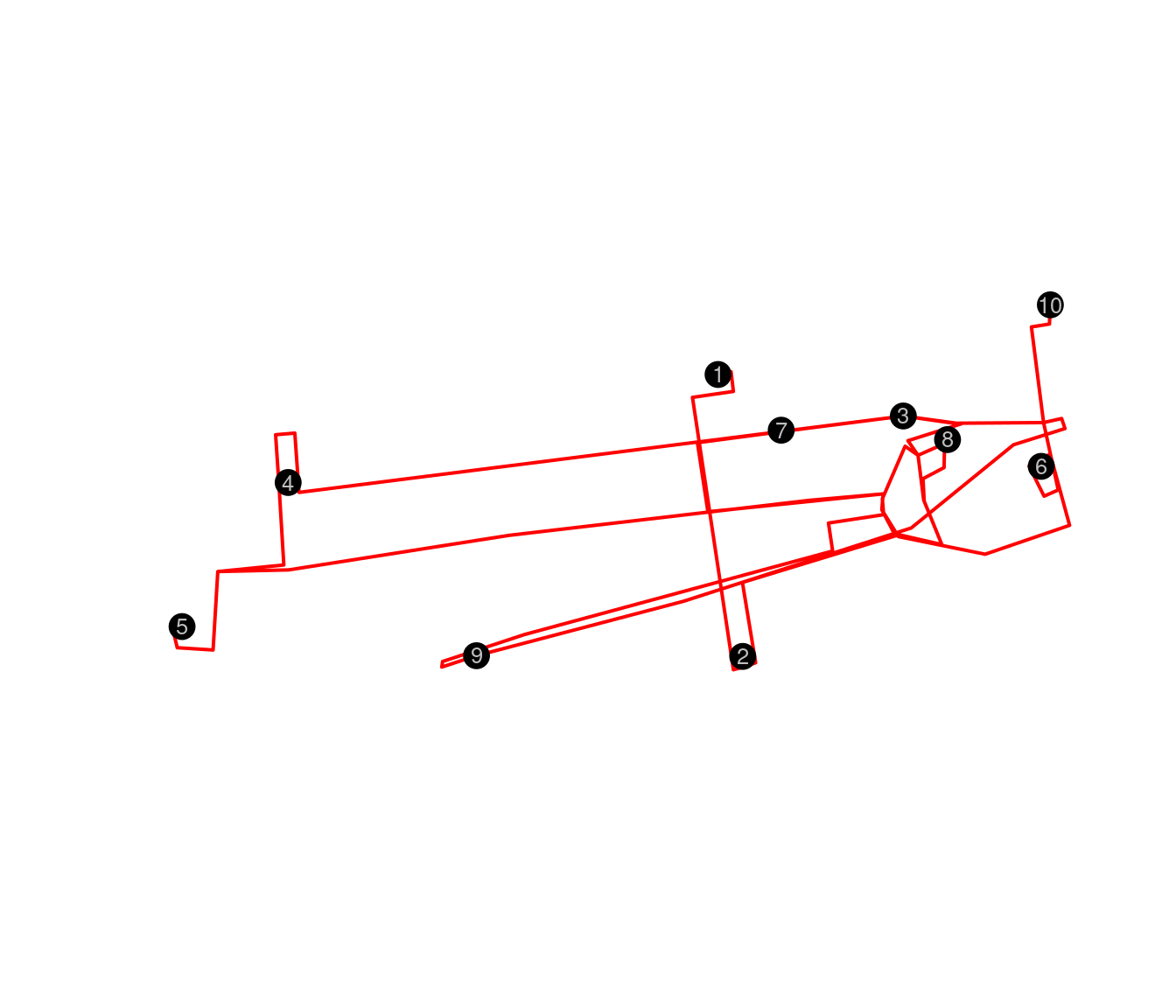

Ruta entre los museos sin optimizar

En la Figura es necesario mencionar que esta ruta no tiene ningun tipo de optimización, pues solamente mostramos el funcionamiento del OSRM, en este caso no hay ordenamiento.

Relizamos la visualización para un mapa interactivo visible en HTML.

library(htmlwidgets)
library(webshot)

# Misma visualización, pero en mapa interactivo.
m<-leaflet(data = sf::st_geometry(ruta1)) %>% 
  setView(lng = mean(locs$lon), lat =mean(locs$lat), zoom = 14) %>%
  addTiles() %>% 
  addMarkers(lng = locs$lon, lat = locs$lat, popup = locs$id) %>%
  addPolylines()
m

Mapa de los puntos sin optimizar

En la Figura , es evidente que la visualización interactiva mediante leaflet es una gran ventaja, (aunque en este documento en pdf no se aprecia) ya que nos permite construir un archivo final html facil de automatizar y al mismo tiempo, conveniente para compartir y visualizar, pudiendo estos ser utilizados desde equipos móviles.

Algoritmo Génetico sobre OSRM

Una vez que definimos que usaremos las ventajas resolutivas mediante AG, el proceso matématico que nos permitirá la construcción de la solución, nos queda hacer la implementación.

Al objeto geodato se le agrega un identificador con ID y nombres en caso que existan, para efecto de este ejercicio vamos a considerar ID y nombres como equivalentes. Se construye la matriz de distancias mediante la función osrmTable de la librería OSRM, luego se transforma a un objeto dist de R, para luego agregar los nombres en dicha matriz de distancias.

#Creamos el identificador de los puntos
geodato$ID<-1:10
nombres<-1:10

# Construimos la matriz de distancias considerando
# el sentido de las calles mediante la función osrmTable
ma_dist <- osrmTable(loc = geodato[1:10, c("ID","lon","lat")])

# Lo llevamos a un objeto dist de R y nombramos los puntos
bd<-as.dist(ma_dist$durations)
bd<-usedist::dist_setNames(bd, nombres)

Se carga la libreria GA para resolver el orden del tour. Se crea una semilla y luego se transforma dicha matriz de distancia en un objetivo tipo matrix de R. Se crean además, la función que medirá el largo del tour, la función de ajuste, la función del tour, las coordenadas mediante un escalamiento multidimensional, el número de iteraciones con la matriz correspondiente.

# Cargamos la librería del Algoritmo Genético
library(GA)

# Definimos la semilla aleatoria y lo llevamos a una matriz
set.seed(123)
D <- as.matrix(bd)

# dado un tour, calculamos la distancia total
tourLength <- function(tour, distMatrix) {
  tour <- c(tour, tour[1])
  route <- embed(tour, 2)[, 2:1]
  sum(distMatrix[route])
}

# la inversa de la distancia total es el ajuste
tpsFitness <- function(tour, ...) 1/tourLength(tour, ...)

# Creamos la funcion del tour
getAdj <- function(tour) {
  n <- length(tour)
  from <- tour[1:(n - 1)]
  to <- tour[2:n]
  m <- n - 1
  A <- matrix(0, m, m)
  A[cbind(from, to)] <- 1
  A <- A + t(A)
  return(A)
}

# coordenadas en 2-d mediante escalamiento multidimensional
mds <- cmdscale(bd)
x <- mds[, 1]
y <- -mds[, 2]
n <- length(x)

# Definimos el número de iteraciones
B <- 100
fitnessMat <- matrix(0, B, 2)
A <- matrix(0, n, n)

Compilamos los resultados del total de iteraciones para luego identificar la ruta mas ajustada. Además se agrega un medidor del tiempo total del proceso.

inicio1<-Sys.time()

for (b in seq(1, B)) {
  # ejecuta el AG
  AG.rep <- ga(type = "permutation", fitness = tpsFitness, distMatrix = D, 
               min = 1, max = attr(bd, "Size"), popSize = 10, maxiter = 50,
               run = 100, pmutation = 0.2, monitor = NULL)
  
  tour <- AG.rep@solution[1, ]
  tour <- c(tour, tour[1])
  fitnessMat[b, 1] <- AG.rep@best[AG.rep@iter]
  fitnessMat[b, 2] <- AG.rep@mean[AG.rep@iter]
  A <- A + getAdj(tour)
}

final1<-Sys.time()
(final1-inicio1)

## Time difference of 9.249091148 secs

Se construye una función para visualizar el orden del tour en matriz de distancias.

plot.tour <- function(x, y, A) {
  n <- nrow(A)
  for (ii in seq(2, n)) {
    for (jj in seq(1, ii)) {
      w <- A[ii, jj]
      if (w > 0) 
        lines(x[c(ii, jj)], y[c(ii, jj)], lwd = w, col = "lightgray")
    }
  }
}

# Graficamos los puntos y la ruta ajusta entre ellos
plot(x, y, type = "n", asp = 1, xlab = "", ylab = "", main = "Tour ordenado")
points(x, y, pch = 16, cex = 1, col = "blue3")
abline(h = pretty(range(x), 10), v = pretty(range(y), 10), col = "lightgrey")
tour <- AG.rep@solution[1, ]
#tour <- ruta[-11,1]
tour <- c(tour, tour[1])
n <- length(tour)
arrows(x[tour[-n]], y[tour[-n]], x[tour[-1]], y[tour[-1]],
       length = 0.15, angle = 45, col = "green4", lwd = 2)
text(x+0.2, y+0.3 , nombres, cex = 1)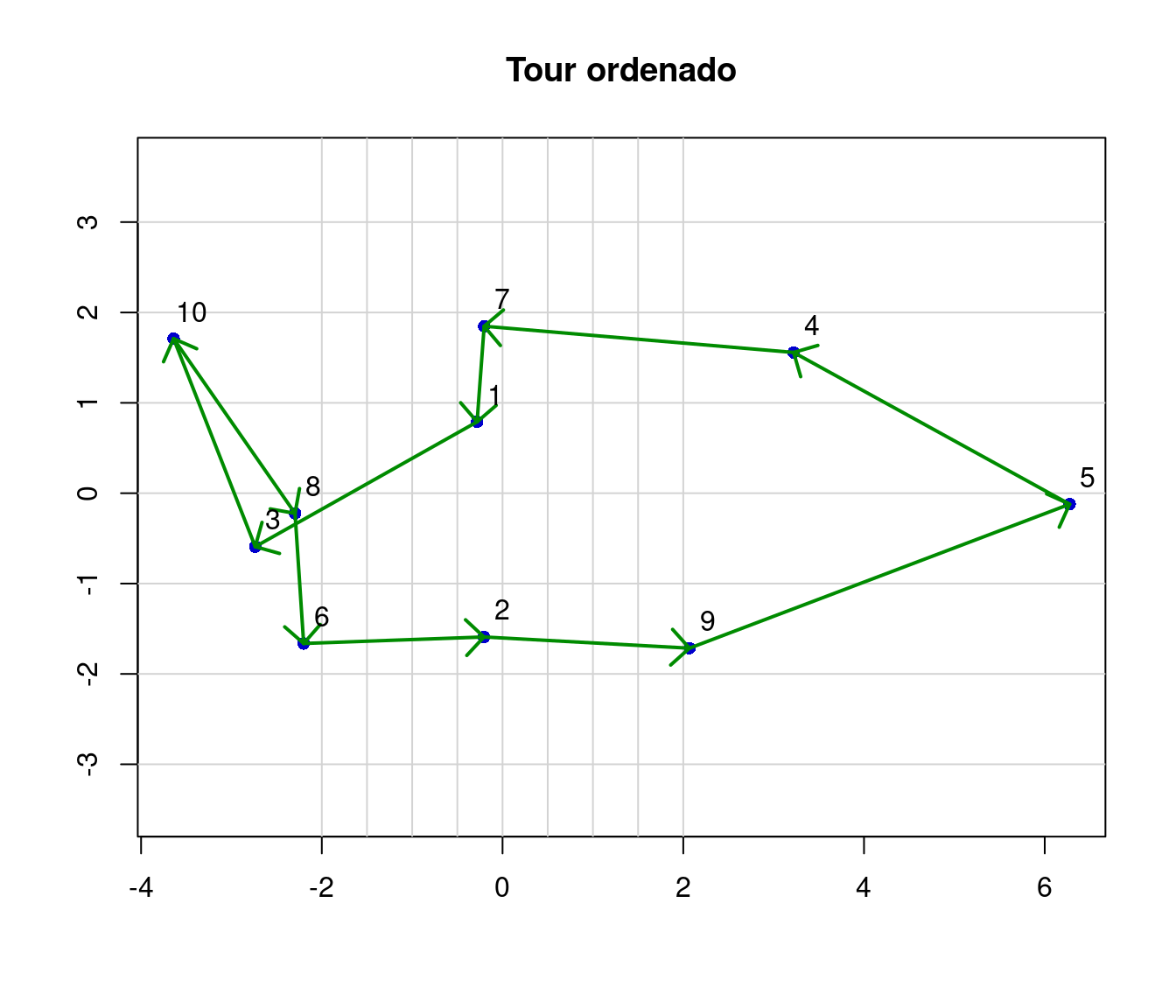

gráfico de los puntos y la mejor ruta que se ajusta entre los puntos

En la Figura , se visualiza el tour ordenado para un recolector de datos en terreno. Este tour esta construido en base a la matriz de distancias.

# Resumen de la progresión del AG
summary(AG.rep)

## $type
## [1] "permutation"
## 
## $popSize
## [1] 10
## 
## $maxiter
## [1] 50
## 
## $elistism
## [1] 1
## 
## $pcrossover
## [1] 0.8
## 
## $pmutation
## [1] 0.2
## 
## $domain
## NULL
## 
## $suggestions
## NULL
## 
## $iter
## [1] 50
## 
## $fitness
## [1] 0.03401360544
## 
## $solution
##      x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
## [1,]  9  5  4  7  1  3 10  8  6   2
## 
## attr(,"class")
## [1] "summary.ga"

plot(AG.rep, main = "progresión de AG")
points(rep(30, B), fitnessMat[, 1], pch = 16, col = "lightgrey")
points(rep(35, B), fitnessMat[, 2], pch = 17, col = "black")
title(main = "50 primeras iteraciones sobre el total de 100 simulaciones
      (mejor y promedio)")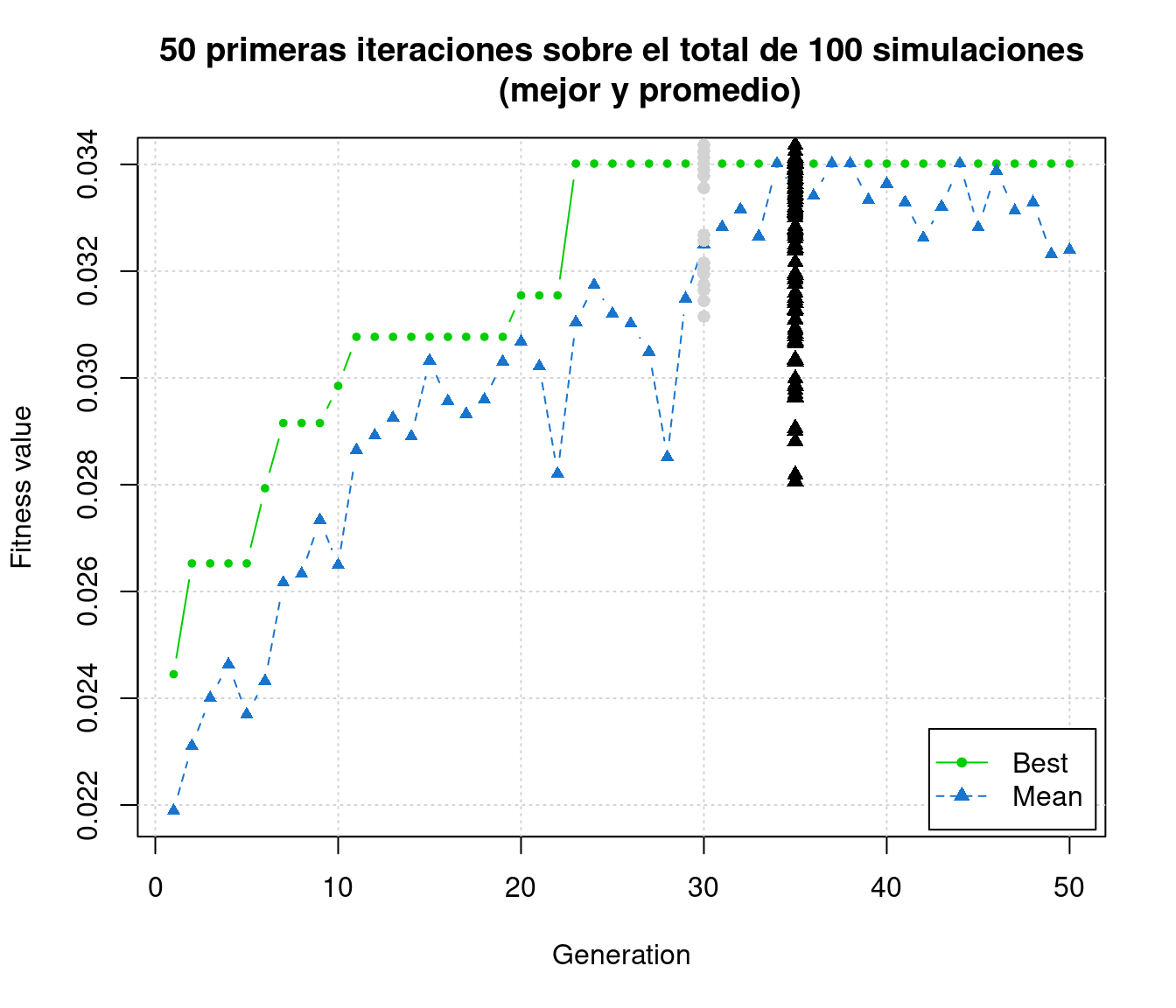

50 primeras iteraciones sobre el total de 100 simulations (mejor y promedio)

En la Figura , visualizamos las 50 primeras iteraciones. El gráfico describle el valor del fitness o ajuste de la función del algoritmo genético en función del número de generaciones. En este caso hicimos un total de 100 simulaciones. Es importante notar que cuando construimos el objeto AG.rep mediante funcion ga se utilizo el argumento maxiter=50, con el fin de definir el número total de iteraciones para cada algoritmo genético. Por lo tanto, aquí se muestra el promedio y la mejor de esas 100 simulaciones, los que tienden a converger entre la generación 30 y 40. Este proceso es el que le confiere una conducta de aprendizaje a esta solución.

plot(x, y, type = "n", asp = 1, xlab = "", ylab = "",
main = "Ruta final seleccionada
     (100 simulaciones)")
plot.tour(x, y, A * 10/max(A))
points(x, y, pch = 16, cex = 1.5, col = "blue")
text(x, y, nombres, cex = 1)
lines(x[tour], y[tour], col = "red", lwd = 1)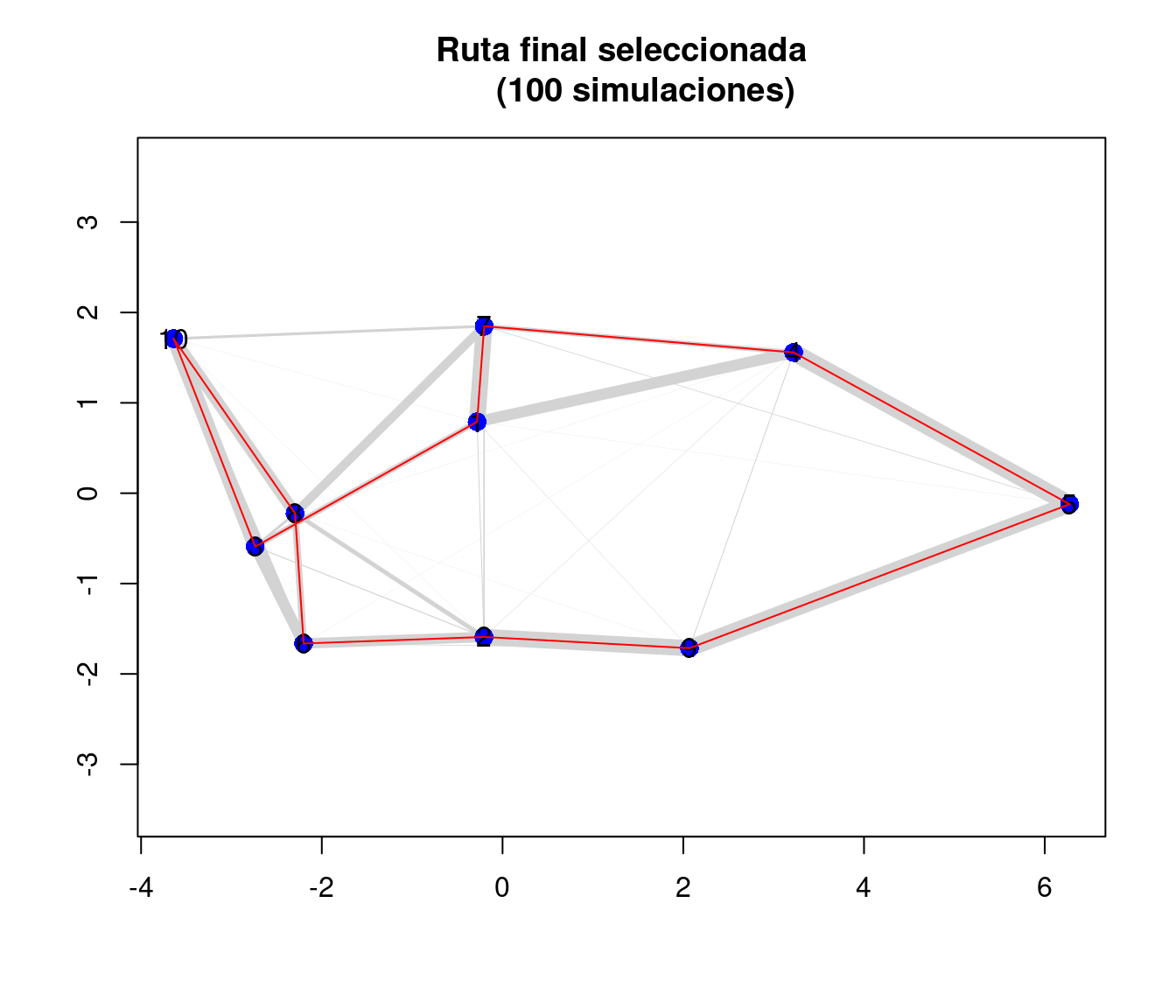

Gráfico del resultado de la mejor ruta

En la Figura , visualizamos en rojo la ruta final seleccionada. En este gráfico es posible visualizar en color gris representa la proporción de los recorridos probados en el total de 100 simulaciones. Por lo tanto, el ancho del trayecto entre los puntos indica que tan eficiente fue esa ruta.

En esta etapa obtenemos la solución y la comparamos con la solución del tour con el fin de validar los resultados. Por lo tanto, ambas deben tener el mismo orden.

# Construccion del vector resultante
nombres_ordenados<-summary(AG.rep)$solution

#ordenamiento del vector

for (i in 1:length(tour[-11])){
  nombres_ordenados[i] <- print(nombres[tour[-11][i]])
}

## [1] 9
## [1] 5
## [1] 4
## [1] 7
## [1] 1
## [1] 3
## [1] 10
## [1] 8
## [1] 6
## [1] 2

# creación del data frame y verificación
posiciones<-data.frame(tour=tour[-11], ID=as.numeric(nombres_ordenados))

# ordenamiento de los puntos de entrada
library(dplyr)
options(digits=10)
bd3<-left_join(posiciones, geodato, by="ID")

En esta etapa cargamos la libreria osrm para luego hacer la conexión con el servidor osrm donde hemos implementado el motor de rutas (OSRM) mediante Docker.

# carga de la librería osrm
library(osrm)
#options(osrm.server = "http://127.0.0.1:5000/")
locs <- structure(
  list(id=bd3$ID,lon = bd3$lon, 
       lat = bd3$lat), 
  class = "data.frame", row.names = c(NA, -10L))

Nuevamente se estima una ruta entre los puntos espacialmente usando la función osrmRoute del motor de rutas. En este caso, el ordenamiento entregado esta definido por el proceso de optimización previamente ejecutado.

ruta1 <- osrmRoute(loc = locs, returnclass = "sf")
plot(st_geometry(ruta1), col = "red", lwd = 2)
points(locs[,2:3], pch = 20, cex = 3)
text(locs[,2:3],as.character(row.names(geodato)), cex = .8, col="grey")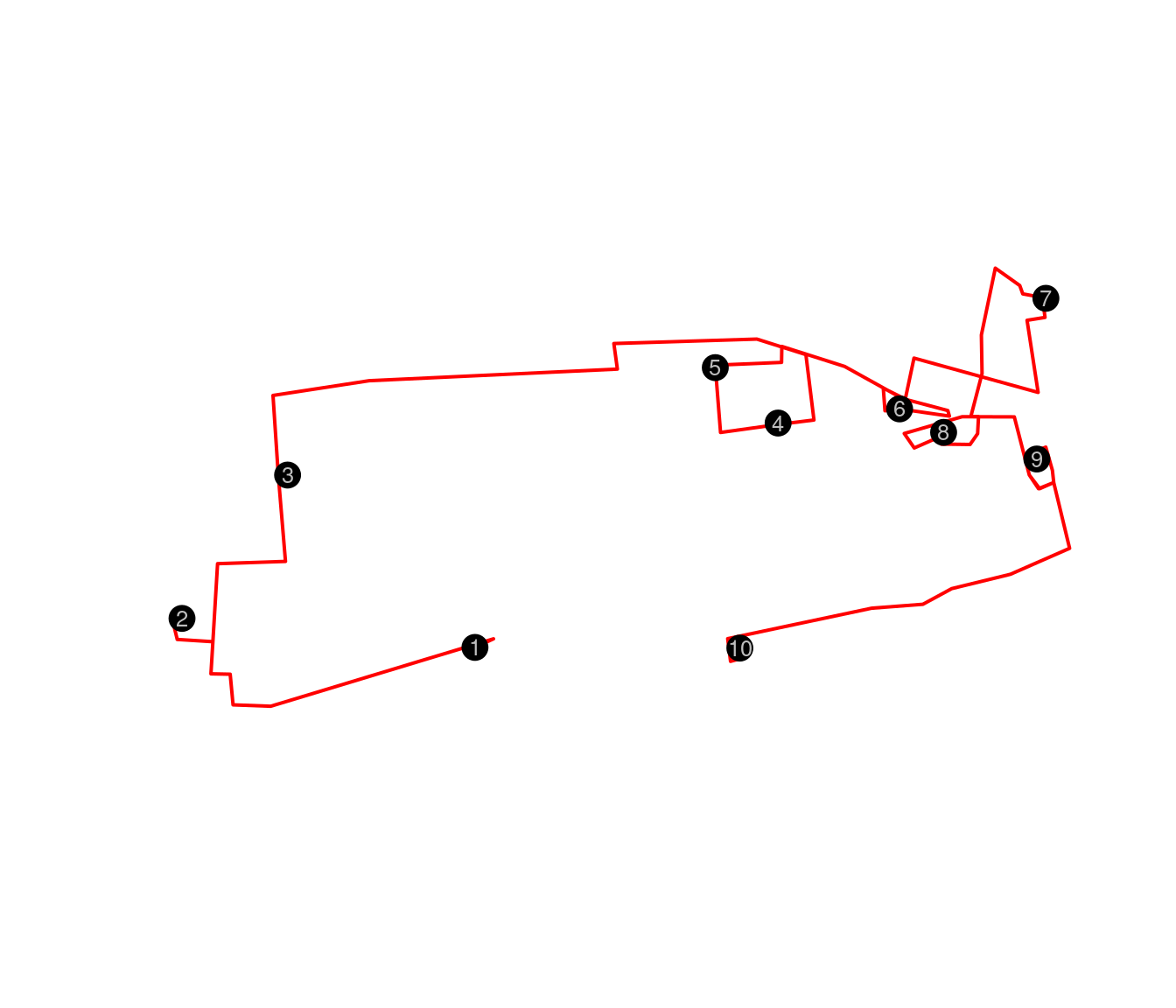

Ruta entre los museos con la optimización AG

En la Figura la ruta optimimizada muestra el recorrido por las calles usando OSRM, pero sin mostrar el contexto.

## load packages
library(leaflet)
library(htmlwidgets)
library(webshot)

## creamos el mapa con la ruta
m <- leaflet(data = sf::st_geometry(ruta1)) %>% 
  setView(lng = mean(locs$lon), lat =mean(locs$lat), zoom = 14) %>%
  addTiles() %>% 
  addMarkers(lng = locs$lon, lat = locs$lat, popup = locs$id) %>%
  addPolylines()

m

Mapa de los puntos optimizados y con una ruta real gracias al OSRM

En la Figura la ruta optimimizada muestra el recorrido por las calles usando OSRM, pero mostrando el contexto en un plano interactivo en html. Sin embargo, para efectos de este documento en pdf, dicha interacción no es posible.

Conclusión

El proceso descrito y esquematizado en este documento, muestra una solución factible para la creación de rutas para los recolectores de datos del IPC en terreno. Pudimos evidenciar que la batería de herramientas de manejo de datos que existe y en especial, programas y software de código libre son un actor importante a la hora de crear innovación de alta calidad, pero con bajo costo asociado. Es absolutamente factible crear procesos de optimización de rutas con esta herramienta, la que requiere un entrenamiento acotado en el caso de hacer capacitación a equipos de desarrolladores de software.

Es importante hacer notar que, para este problema, el resultado optimizado cumple con los requisitos de ser una optimización de calidad y tal como se muestra en los hallazgos del informe “Rutas óptimas para recolectores de IPC” existe una reducción del 15% en los tiempos de viaje de las rutas que hicieron los recolectores de datos en años previos.

Este algoritmo funciona bien cuando se trabaja con no más de 50 puntos a recorrer. Sería muy raro que un recolector de datos deba cubrir más de 15 lugares al día durante su jornada laboral. Por lo general, ese recorrido se realiza entre 10 y 15 establecimientos en su tiempo de trabajo. Por lo tanto, para efectos de resolver este problema en estos términos, los resultados son convenientes en la reducción del tiempo total.

Por otro lado, y en relación a aspectos técnicos del proceso en R, la implementación de Docker y OSRM no nos mostraron grandes dificultades. Si bien estos resultados no son una innovación científica de primera línea, juntar, combinar y sinergizar los procesos que se muestran aquí, lo hace una innovación. No está de más decir que sacamos ventaja de quienes por filosofía ponen a disposición del público el desarrollo de sus trabajos, como el caso del proyecto OSRM u OSM. Herramientas que se hacen parte de un esquema de trabajo colaborativo y benéfico para todas las partes. La comunidad del software libre y de la filosofía del código abierto fomenta este tipo de trabajos.

Por último, hacer notar que en esta etapa hemos trabajado durante el 2020. Sin embargo, este año 2021 tenemos mucho interés para seguir estudiando y conociendo herramientas que nos permitan empaquetar todo este proceso en un servidor local de la institución, para poder dejar disponible una herramienta que permita resolver consultas de optimización de rutas para la institución y mejorar la recolección de datos en terreno, pero quizás si el proyecto crece en el tiempo también puede ayudar y servir a las necesidades de todas las instituciones del Estado. Principalmente, pensado que esta herramienta no es solo útil para el Instituto Nacional de Estadísticas (INE-Chile), sino que, para los ministerios, municipalidades y en especial, para lograr distribuir con mayor precisión la ayuda social y medicamentos que la población necesita en estos tiempos de contingencia sanitaria.

Bibliografia

Applegate, David, Robert Bixby, Vašek Chvátal, and William Cook. 2003. “Implementing the Dantzig-Fulkerson-Johnson Algorithm for Large Traveling Salesman Problems.” Mathematical Programming 97 (1): 91–153.

Applegate, David, Robert Bixby, William Cook, and Vasek Chvátal. 1998. “On the Solution of Traveling Salesman Problems.”

Bennett, Jonathan. 2010. OpenStreetMap. Packt Publishing Ltd.

Bittinger, Kyle. 2020. Usedist: Distance Matrix Utilities. https://CRAN.R-project.org/package=usedist.

Bivand, Roger S., Edzer Pebesma, and Virgilio Gomez-Rubio. 2013. Applied Spatial Data Analysis with R, Second Edition. Springer, NY. https://asdar-book.org/.

Boettiger, Carl. 2015. “An Introduction to Docker for Reproducible Research.” ACM SIGOPS Operating Systems Review 49 (1): 71–79.

Cheng, Joe, Bhaskar Karambelkar, and Yihui Xie. 2019. Leaflet: Create Interactive Web Maps with the JavaScript ’Leaflet’ Library. https://CRAN.R-project.org/package=leaflet.

Darwin, Charles. 1859. “The Origin of Species and the Descent of Man, New York (the Modern Library).”

Detomasi, Richard, Gabriela Mathieu, and Germán Botto. 2018. “EPP v. 0.2: Evaluation of Proximity Programs with OSRM Routing.” In Conferencia Latinoamericana Sobre Uso de r En Investigación+ Desarrollo (LatinR 2018)-JAIIO 47 (CABA, 2018).

Flood, Merrill M. 1956. “The Traveling-Salesman Problem.” Operations Research 4 (1): 61–75.

Giraud, Timothée. 2020. Osrm: Interface Between r and the OpenStreetMap-Based Routing Service OSRM. https://CRAN.R-project.org/package=osrm.

Holland, John. 1975. “Adaptation in Natural and Artificial Systems: An Introductory Analysis with Application to Biology.” Control and Artificial Intelligence.

Huber, Stephan, and Christoph Rust. 2016. “Calculate Travel Time and Distance with OpenStreetMap Data Using the Open Source Routing Machine (OSRM).” The Stata Journal 16 (2): 416–23.

Jaffee, David. 1996. “One Hundred Years on the Road: The Traveling Salesman in American Culture.” JSTOR.

Little, John DC, Katta G Murty, Dura W Sweeney, and Caroline Karel. 1963. “An Algorithm for the Traveling Salesman Problem.” Operations Research 11 (6): 972–89.

Mirjalili, Seyedali. 2019. “Genetic Algorithm.” In Evolutionary Algorithms and Neural Networks, 43–55. Springer.

Pebesma, Edzer. 2018. “Simple Features for R: Standardized Support for Spatial Vector Data.” The R Journal 10 (1): 439–46. https://doi.org/10.32614/RJ-2018-009.

Petersen, Richard. 2020. Ubuntu 20.04 LTS Desktop: Applications and Administration. surfing turtle press.

R Core Team. 2020. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Raggi, Emilio, Keir Thomas, and Sander Van Vugt. 2011. Beginning Ubuntu Linux. Springer.

Scrucca, Luca. 2012. “GA: A Package for Genetic Algorithms in r.” Submitted to Journal of Statistical Software.

Tennekes, Martijn. 2020. Tmaptools: Thematic Map Tools. https://CRAN.R-project.org/package=tmaptools.

Wickham, Hadley, and Jennifer Bryan. 2019. Readxl: Read Excel Files. https://CRAN.R-project.org/package=readxl.

Wickham, Hadley, Romain François, Lionel Henry, and Kirill Müller. 2020. Dplyr: A Grammar of Data Manipulation. https://CRAN.R-project.org/package=dplyr.

---

1. R Core Team (2020). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.↩︎

2. Scrucca, L. (2012). GA: A Package for Genetic Algorithms in R. Submitted to Journal of Statistical Software↩︎

3. https://github.com/Project-OSRM/osrm-backend↩︎

4. https://www.docker.com/↩︎

5. https://releases.ubuntu.com/20.10/↩︎

6. https://operations.osmfoundation.org/policies/nominatim/↩︎

7. https://wiki.osmfoundation.org/wiki/Main_Page↩︎

8. Luxen, D., & Vetter, C. (2011, November). Real-time routing with OpenStreetMap data. In Proceedings of the 19th ACM SIGSPATIAL international conference on advances in geographic information systems (pp. 513-516).↩︎

Copyright © 2021 SIE-INE, Attribution-ShareAlike 3.0 IGO. Contacto rutasoptimas at gmail.com